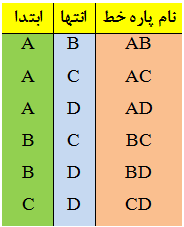
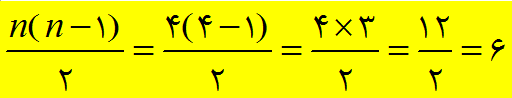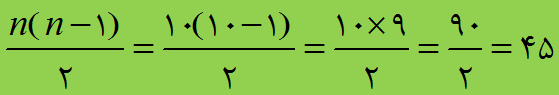قطر پاره خطی است که دو زاویه ی غیر مجاور را در چندضلعی ها به هم وصل میکند.
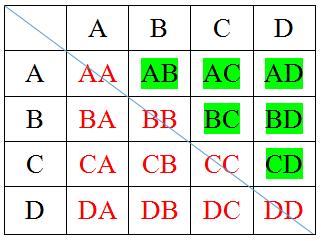
زوایای مجاور چندضلعی وقتی است که یک ضلع مشترک داشته باشند مثلا زوایای B و C در یک ضلع مشترک هستند مجاور هم هستند ولی زوایای B و D ضلع مشترک ندارند پس غیرمجاور و بین آنها میتوان قطر رسم کرد.
پیدا کردن قطر همانند پیدا کردن پاره خط است که میتوان از روش های پیدا کردن پاره خط استفاده کرد:
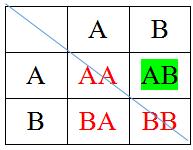
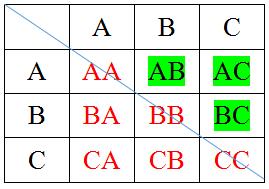
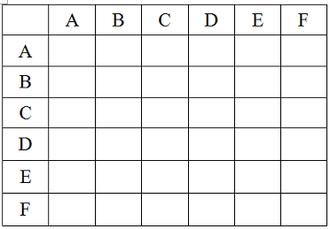
روش جدول نظام دار:
|
قطر چندضلعی |
زاویه انتها |
زاویه ابتدا |
|
AC |
C |
A |
|
AD |
D |
A |
|
AE |
E |
A |
|
BD |
D |
B |
|
BE |
E |
B |
|
BF |
F |
B |
|
CE |
E |
C |
|
CF |
F |
C |
|
DF |
F |
D |
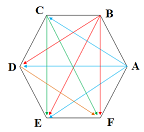
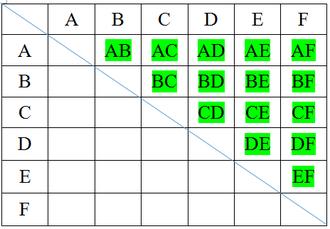
قطرها عبارتند از:
AC, AD, AE, BD, BE, BF, CE, CF, DF
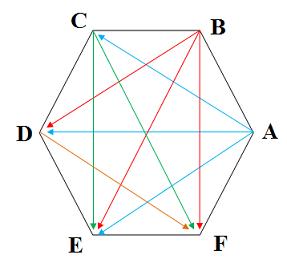
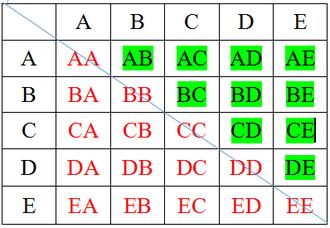
زوایای غیرمجاور A عبارتند از: C,D,E که قطرهای AC, AD, AE را تشکیل میدهند که با رنگ آبی نشان داده شده اند.
زوایای غیرمجاور B عبارتند از: D,E,F که قطرهای را BD, BE, BF تشکیل میدهند که با رنگ قرمز نشان داده شده اند.
زوایای غیرمجاور C عبارتند از: E,F که قطرهای CE,CF را تشکیل میدهند که با رنگ سبز نشان داده شده اند.
زاویه غیر مجاور D عبارت از: F که قطر DF را تشکیل میدهد که با رنگ نارنجی نشان داده شده است.
روش فرمول برای شمارش قطر داخلی چندضلعی:
برای شش ضلعی داریم:
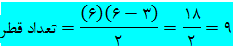
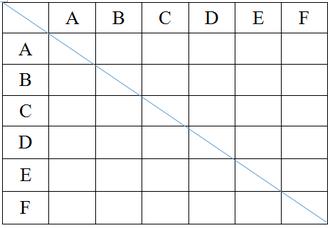
n همان تعداد نقاط است.
